Making 5 and 10

One of the most powerful and flexible early joining strategies is to learn to make and use fives and tens. Ten anchors our number system because humans have 10 fingers, and with five on each hand, half of ten becomes a springboard into base ten thinking. Connecting five and ten to our fingers – the original manipulatives – is critical to understanding our number system and seeing (and feeling) how numbers can be composed and decomposed. As you give students experience with their fingers, help them begin to abstract the ideas of five and ten using other manipulatives, like the dice in our image of the week. Take a moment and look at this image. How many do you see? What different ways might your students see how many are in this image?

Notice first that students might choose to focus on the dice as the units to count. There are 10 dice here altogether, but it is likely that students might see these ten as smaller groups first. Perhaps they see five on the left (made of four green dice and one orange) and five on the left (made of four white dice and one purple). In doing so, students would be composing and decomposing both five and ten: 5 = 4 + 1 and 10 = 5 + 5.

But if your students use the dots as units, there are even more ways to use five and ten to answer the question, How many? Look at just a few ways shown below.

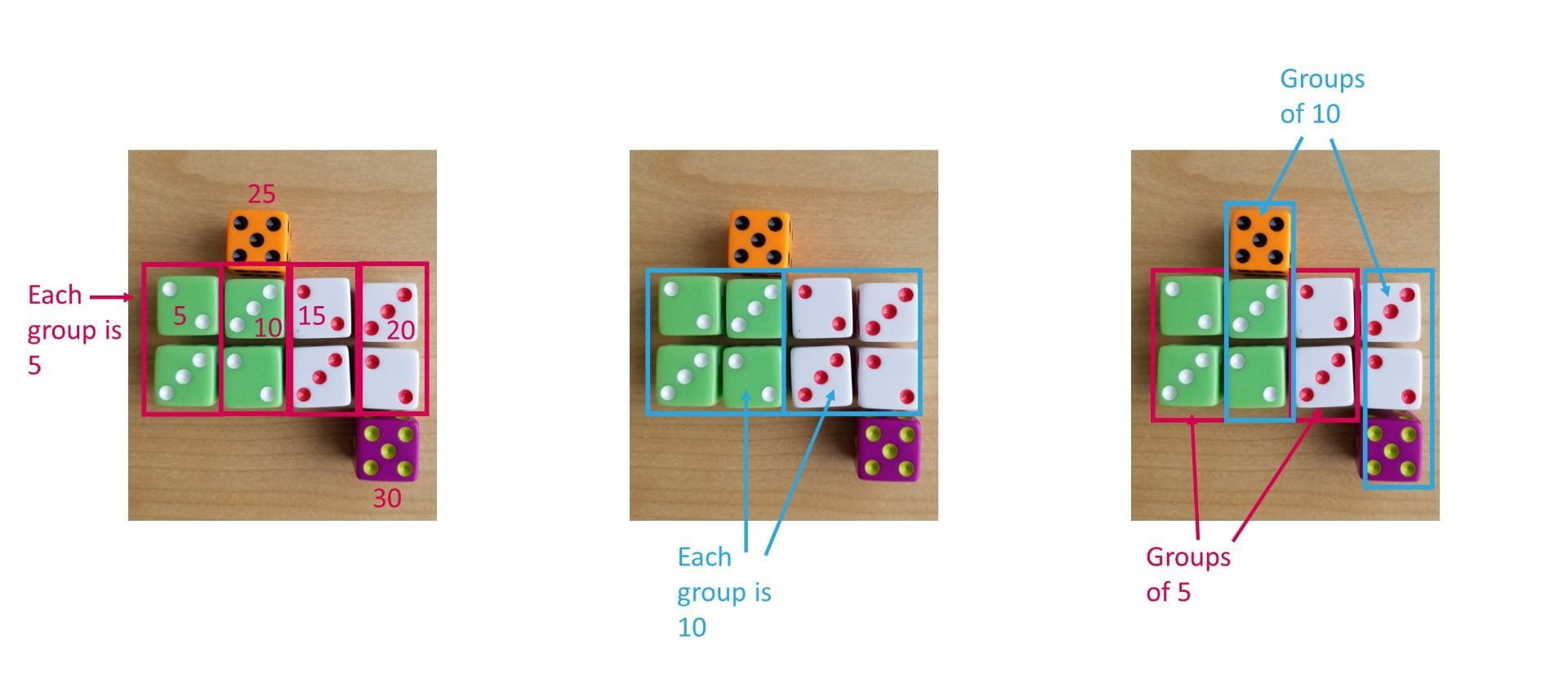
Once students begin to see 5 or 10, then they need ways of joining them to find how many dots there are altogether. On the left image you can see one way a student might use skip counting – an efficient and practical strategy when all the groups are the same size. Alternatively, students might form groups of ten and then count on by fives: 10, 20, 25, 30. Older students might think multiplicatively, seeing this as 6 group of 5, or 6 x 5 = 30.

As an extension, ask students, How could you extend this pattern? How many dots would there be then? How do you know? If you have access to dice, students can construct and extend this pattern. If not, students can simply draw and extend the pattern. For older students, consider asking questions like, If you extend this pattern, how many dice would you need for there to be 100 dots? How do you know?

So many big ideas open up when we start by building 5 and 10! Try this or any of our other Making 5 and 10 activities with your students tomorrow.

And we invite you to follow us on Twitter! Tweet us the fascinating ideas you students have about our activities or how you’re trying these activities in your space. We can’t wait to hear from you!

To multiplicity, cheers!

Jen Munson and the multiplicity lab group