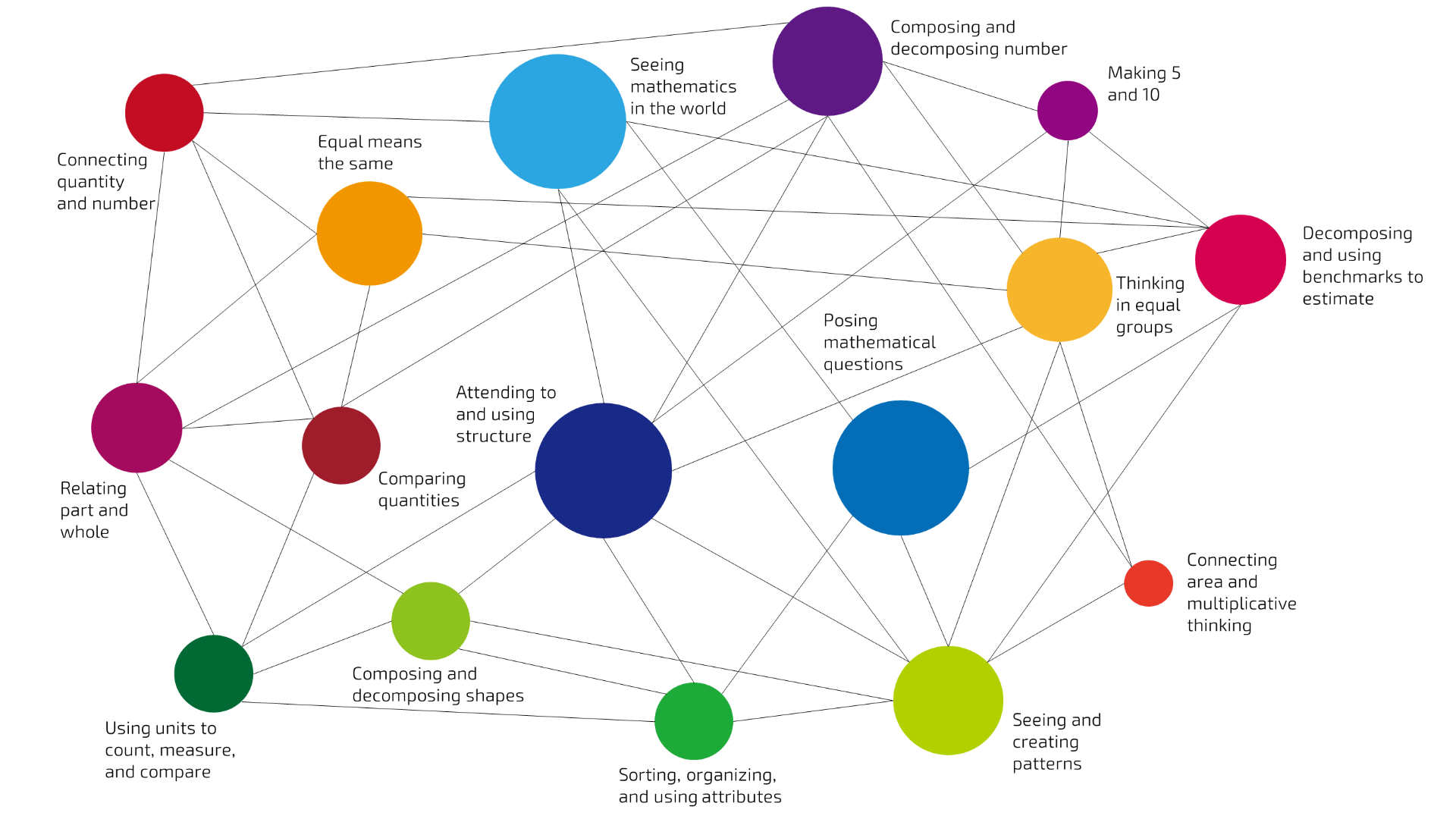
Big Ideas
Mathematical Concepts and Practices Embedded in Our ActivitiesSeeing mathematics in the world
Learning to see mathematics as living in our world is a central mathematical practice, one that has been historically neglected. Mathematics is not a purely abstract, procedural pursuit, but, rather, a way of understanding our world. Children will more deeply understand other big ideas if they see them as connected to their own lived experiences. We want children to walk through their home, school, and neighborhood noticing the patterns we use to construct each, the ways that numbers are visible in the arrangements of objects, and how sorting the world by attributes can help us understand it. As a mathematical practice, or a way of approaching mathematical work, rather than a concept, seeing mathematics in the world is connected to all other big ideas, enriching the ways we can understand each.
Posing mathematical questions
Related to seeing mathematics in the world, posing mathematical questions is a practice that support the understanding of all other big ideas. In schools, we typically position the teacher or curriculum as the askers of questions and students as the answerers. But learning to ask questions is perhaps even more important than finding the answers. Further, encouraging students to pose mathematical questions, to wonder, positions them with the agency to be in a two-way conversation with mathematics. When students ask the questions, they are far more engaged in finding the answers. And they may ask more challenging, insightful, and meaningful questions than we as teachers or the curriculum would have dared.
Attending to and using structure
Attending to and using structure is an often-overlooked mathematical practice in elementary grades, but it is inherently what we want students of all ages to be doing and learning to do all the time. Attending to structure involves noticing how numbers, objects, and patterns are put together, arranged, and related. From learning that the number six has a particular structure on a die to noticing that checkerboards are made from alternating colored squares, attending to structure gives students access to the mathematical ideas embedded in our world. Students use structure when they leverage what they notice to do something mathematical, such as knowing how many spaces to move in a game or create their own pattern with blocks. Structure allows us all to do a huge variety of useful things, such as use place value, keep rhythm, layout cookies on a baking tray, and make predictions.
Connecting number and quantity
Counting is a complex endeavor that begins before students enter school. To count, children need to connect and coordinate number words and a quantity of objects. This involves (1) knowing the sequence of counting words, (2) understanding that those words represent quantities, (3) using one-to-one correspondence to match each object with a single number word, (4) cardinality, or knowing that, when counting a group, the last number word said represents the quantity in the entire set, and (5) conservation, or knowing that no matter what order the objects in a set are counted in, the number should be the same. Beyond this dizzying group of concepts, children are also learning that a single number, such as four, can represent wildly different things, from four legs on a table or four people, to four grapes or four leaves. The activities that focus on this big idea encourage students to move beyond counting as an oral sequence of words to connecting those words to the objects they are meant to represent, building a sense of each number as a quantity.
Comparing quantities
Learning to count goes hand-in-hand with learning to compare. Children naturally make comparisons all the time to learn about their world, and as counting opens up to them, making comparisons based on quantity is a logical progression. Comparing quantities involves both precise comparisons and estimations, both of which are important and support the other. Students learn why one number is more than another, but using the counting sequence, building sets, and comparing lengths of objects in a line. Each of these can be used to justify a comparison. Children also need to exercise their capacities for estimating quantities for comparison, assessing the size of the objects, the space each group takes up, and how the objects are arranged. Each of these factors connects to big ideas later, such as density, area, and volume.
Equal means the same
Just as students learn to compare quantities, expecting one to be more than the other, they must simultaneously grapple with the meaning of equal. Equality means that two or more sets have the same value, in whatever way that is defined. Equal can refer to the same number value, as with the two expressions that make up the equation 5 + 5 = 8 + 2, or that they have the same quantity of a particular attribute, such as length or weight. What equal does not imply is congruence, or that they two sets appear identical. This can be perplexing precisely because there are so many attributes to compare; it can be easy to focus on comparing a surface feature rather than the underlying value. Developing ideas about equality are essential for all mathematical work, and to do so students need to discuss why two sets are equal (or not) and justify what attributes they are comparing when they make this claim.
Composing and decomposing number
Composing and decomposing number is a very big idea, indeed, involving ideas about joining and separating numbers, in any operation. Students are working on this big idea when they enter school, and they are continuing to develop strategies as they exit elementary school. Students learn to see that groups can be put together and taken apart in a wide variety of ways, including creating sets of physical objects, drawing pictures and number lines, thinking in tens and ones, and using known facts. These strategies develop and adapt across years as students learn more about the patterns in numbers, confront new types of problems, and the quantities they work with grow. For a complete treatise on students’ developmental trajectories and how to support them, we highly recommend Carpenter, Fennema, Franke, Levi, and Empson’s (2015) Children’s Mathematics: Cognitively Guided Instruction. In our activities, which focus on interpreting mathematics visually, one key idea students develop is subitizing, or recognizing small quantities (1 – 6 objects) without counting. Students may not know how many objects there are in a set, but when they begin to see a group of 4, for instance, and a group of 3, they then consider how to join these to find the total.
Making 5 and 10
Making 5 and 10 is a critical subset of composing and decomposing number, in which students focus on building, and, later, building with, groups of five and ten. As students learn to make small group of objects as a way of counting a larger set, they confront needing to count these sets to find the total. Skip counting by fives and tens is a rhythm classrooms of young students should explore, and knowing how to count orally by fives and tens provides a reason to group objects that way for counting. As students later work with numbers, creating a group of five or ten can be part of a larger composing or decomposing process, as when students transform 9 + 4 into 10 + 3 before finding its value as 13. Fives and tens are particularly useful because of our base ten place value system. Learning to work with fives and tens, beginning first with fingers and hands in kindergarten, ultimately supports students in making sense and using place value with larger numbers later.
Relating part and whole
When children consider part and whole together, they are thinking comparatively, inviting in ideas about fractions and ratios. These ideas about rational numbers and proportional reasoning are pivotal to mathematical thinking in middle grades and beyond. It all begins with simple comparisons such as most of, almost all, about half, and less than half. Later, students learn to quantify comparisons using both fractions (in words and numbers) and relationships (such as “8 out of 10”). In each case, students must be simultaneously considering both the part and the whole from which it is taken to understand the relationships between them. In our visual activities, this can involve making comparisons between quantities or areas, both precisely (“two-thirds”) and as an estimation (“about half”). Understanding benchmark fractions of half, third, fourth, and iterations of each is as important as understand benchmark whole numbers, such as 5, 10, and 100.
Decomposing and using benchmarks to estimate
To estimate with a degree of accuracy requires deep understanding of numbers, composing and decomposing of number and space, the units involved, and, often, geometric and measurement ideas, such as density, area, and volume. To estimate often requires coordinating more big ideas than finding a precise answer and should be viewed as a challenging intersection of multiple concepts. To become flexible, versatile estimators, students need experience with a variety of units, from estimating crowds of people and jars of beans, to estimating the distance across a room or the weight of a bucket of water. Estimation often involves two strategic moves that require time to develop: using benchmark quantities and counting small portions and iterating. When students use benchmarks, they might think that they know what 10 pencils or 1 foot looks like and use that as a reference for the unknown. Students might combine this with counting our measuring a portion of the unknown, such as one layer of beans in a jar or a cluster of 10, and then asking, How many of these groups do I think make up the whole? Estimation demands drawing on a complex network of big ideas and, therefore, opens the door to developing many at the same time.
Thinking in equal groups
Multiplication as an operation typically enters the stage in third grade, but students can and should be developing ideas that lead toward multiplicative reasoning from the earliest grades. Indeed, this is what makes thinking in equal groups a big idea. Students begin on this pathway simply to make counting more efficient, counting by twos and, later, by fives and tens. Skip counting is a form of thinking in and with equal groups, and students can use it, along with manipulatives, to solve problems involving repeated sets of objects in kindergarten and first grade. We can connect equal groups to rows and columns in arrays, which we address in the big idea Connecting area and multiplicative thinking. Students use strategies of repeated addition, doubling, and, later, multiplication, to expand the range of tasks involving equal groups they can solve. Multiplication as a procedure is largely the culmination of this effort, not the starting point.
Connecting area and multiplicative thinking
Multiplicative thinking is particularly useful when understanding area, and vice versa. The rows and columns of a rectangular array are equal groups of objects or squares. Finding the total number of them involves thinking about considering which equal groups you want to count (rows or columns) and finding ways to iterate. The total can then be seen as the number of objects, as with eggs in a carton, or the area of the rectangle, as with tiles on a floor. Connecting area and multiplicative thinking also provides a visual proof for the commutative property of multiplication, or why 5 x 7 is equal to 7 x 5. Arrays are used throughout our world to organize objects and area, a key structure that we want students to develop ideas about and be able to use.
Seeing and creating patterns
Mathematics is often described as the study of patterns, and the human brain as a pattern seeker. Patterns are how we learn, connecting ideas that often appear together so we can make predictions about what will happen next. This natural tendency to look for patterns should be a central endeavor in mathematics classrooms starting in preschool. Patterning involves first looking for structures, rhythms, and repetitions and learning to articulate what we see or hear. Children can create their own patterns and learn to extend patterns they find. Seeing and creating patterns as a big idea is tightly coupled with the mathematical practice of attending to and using structure. Patterning can be visual, auditory, physical, or numerical, and finding connections between these different kinds of patterns only strengthens students’ capacity to understand and work with common structures. In our activities, we invite students to look for patterns of all kinds and, later, to extend those patterns and make predictions. These very patterns are the foundation for algebraic thinking and reasoning, which students are beginning to develop long before middle and high school.
Sorting, organizing, and using attributes
Sorting, organizing, and using attributes is the foundation on which all data science is built. When we ask questions that can be answered by data, we are always comparing or tracking change in groups created with shared attributes. Students begin on this data journey, more critical to their capacity to engage in the world now than ever, by first learning to attend to and use the attributes of the things around them. This can include noticing, as we invite students to do, that buttons have attributes like color, size, number of holes, texture, shape, writing, and material, among others. Objects can be sorted, organized, displayed, and compared by these attributes, which can allow us to learn more about them. Organizing in this way is a mathematical activity that can help us see patterns and trends or invite new questions.
Composing and decomposing shapes
Just as understanding and working with numbers involves developing sophisticated ways of joining and separating them, understanding and working with space involves developing ways of composing and decomposing shapes. Seeing what shapes can be made out of component parts, like pattern blocks, or what shapes are hidden inside others requires a visual fluency that can only be developed with time. Some students come to school having spent endless hours building with blocks or doing jigsaw puzzles, developing this visual fluency with each piece rotated, tested, and placed. Other students may have far less experience developing spatial reasoning, so we must create repeated and regular opportunities for students to work with and solve problems that involve space. Spatial reasoning, the larger nest that composing and decomposing shapes sits inside, is linked to patterning, algebraic reasoning, and mathematical thinking of all kinds.
Using units to count, measure, and compare
Connected to understanding and using attributes, using units to count, measure, and compare involves thinking about precisely what is being counted, measured, or compared. Units help us quantify and compare attributes that we might not otherwise be able to, such as length, weight, time, area, and volume. Instead of saying that one jar is bigger than another, students learn to point to a particular attribute (say, the jar’s height or volume) and use units to measure that attribute. Using units, we can make precise comparisons to say not just that one object is, for example, longer than another, but how much longer it is. In this way, this big idea is connected also to composing and decomposing number and comparing quantities.