What’s Missing? Spatial Structuring!

Have a look at the image of the week above for a moment, and ask yourself, How many squares are missing? Pay attention to how your brain is thinking about the task. What did you notice? How did you use your observations?

As adults, we may take it for granted that the array around the empty space in this image shows the dimensions of each side. You might have noticed the five units along the bottom, for example, and mentally extend them upward into the empty space. Or perhaps you noticed the pairs of units along the sides and extend those lines across. You can see both of these ways in the images on the left below. You might have decomposed the shape further by noticing smaller arrays within the empty space: 2 x 2 squares, or a 2 x 5 array along the bottom like a ten frame, or a pair of units hanging out on the right side.

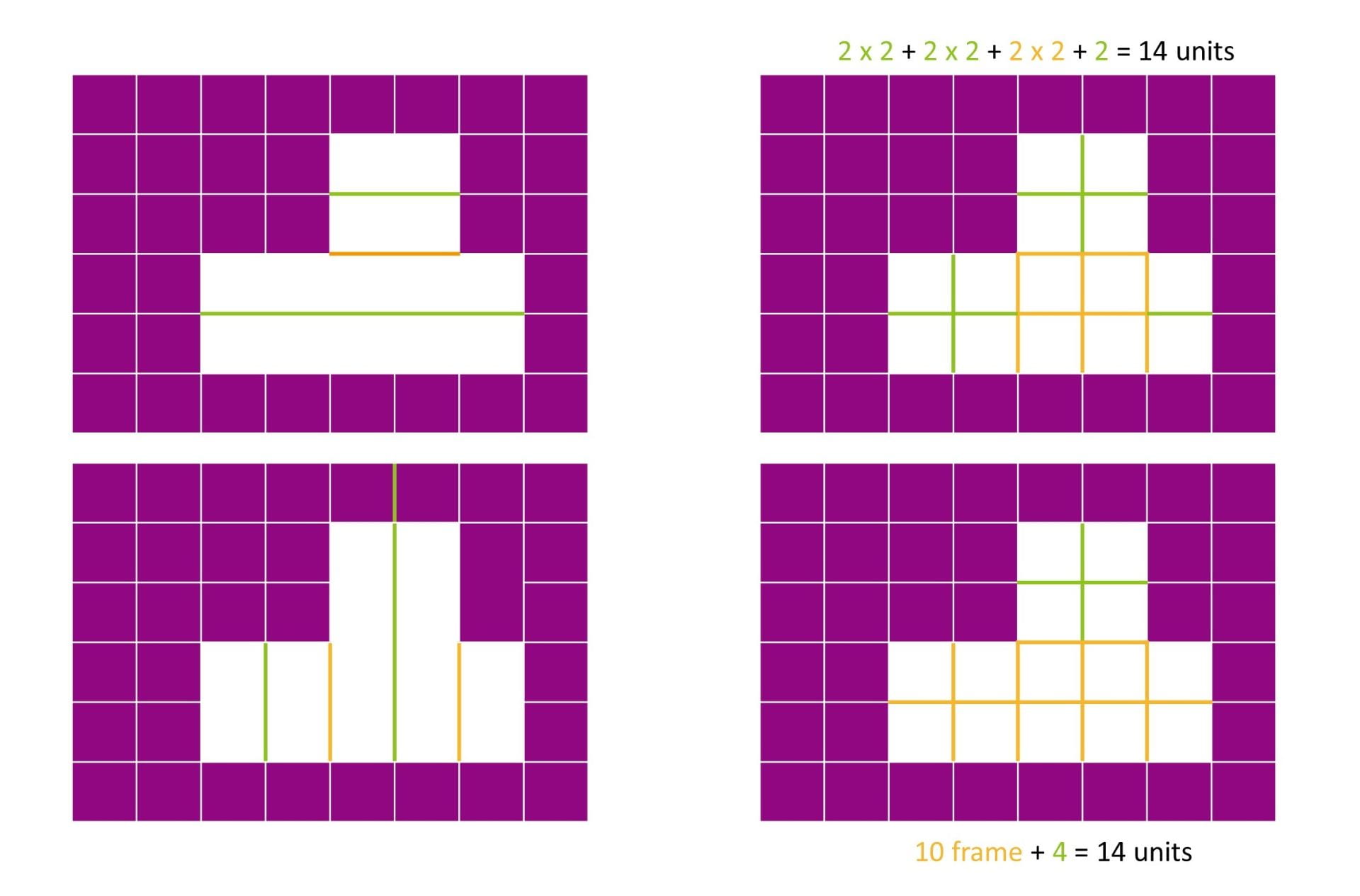
This capacity to mentally organize the space, imposing structure on it to decompose the space into useful components, is called spatial structuring (Battista, 1999; Shumway, 2018). Like many geometric concepts, this is one we never teach or talk about in school, but it is a critical idea for understanding spatial relations and, in the case of our image of the week, area. Area is the number of square units needed to cover a two-dimensional space, and to think about the area of an open space like the one shown in our image of the week, students must be able to impose a row-and-column structure on it when one does not exist. Once students can see that structure, they can use it to decompose the space into useful parts, like the two ways shown on the right of the image above.

When you stop to think about the spatial, organizational, structural, subitizing, and composition work this requires, it’s no wonder figuring out how many squares are missing is so challenging for children. They are integrating many big math ideas at once. To learn to connect and move between these many ideas and learn spatial structuring, students need meaningful opportunities to grapple with these ideas. Try this activity – or any of our spatial structuring activities – with your students and marvel at what they notice, how they reason, and all the ideas they are juggling to do so!

To multiplicity, cheers!

Jen Munson and the multiplicity lab group

References

Battista, M. T. (1999). The importance of spatial structuring. Teaching Children Mathematics, 6(3), 170–177.

Shumway, J. F. (2018) Number sense routines: Building mathematical understanding every day in grades 3-5. Stenhouse.