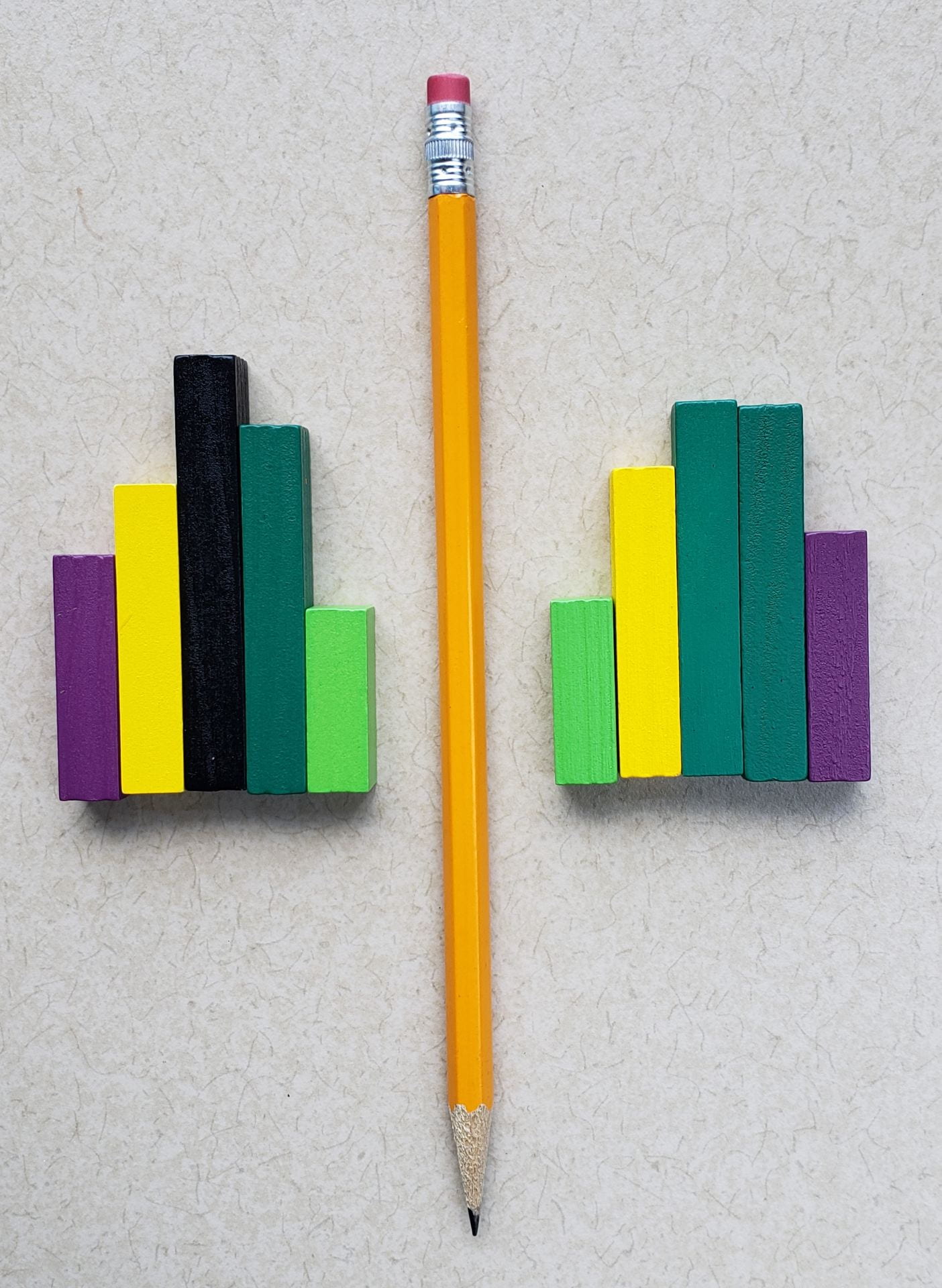Image of the Week: Which is More? with Cuisenaire Rods

Which is More? with Cuisenaire Rods

Last week, we looked at how students might think about the question, Which is more? when they were comparing two groups if dice. With this week’s image, we ask the same question with new manipulatives: Cuisenaire rods. Here at multiplicity lab, we love Cuisenaire rods because of all the relationships between the rod students can explore. Your school may have Cuisenaire rods hidden in a back closet or in a dusty box. Too often these tools go unused, so this year we’re going to look at a few new ways you can use this manipulative.

Look at the two sides of this week’s image: Which is more? Watch for a moment what your mind does. You might at first notice that several of the rods on the two sides are the same, or that there is a taller black rod only on the left. You might then ask yourself, What am I comparing? You might:

• Compare the total number of rods and say that there are five on each side, so the side are equal.
• Compare rods by color and say the sides are equal for yellow, light green, and purple rods. The left has more black rods, and the right has more dark green rods.
• Compare the value (or lengths) of the rods – and this is where things get interesting…

Each Cuisenaire rod has a unit value ranging from one to ten. In this image it is not immediately obvious how long each rod is, though students could use some clues to deduce the values. If students did figure out the values from the image or by recreating and exploring it with Cuisenaire rods in your classroom (time to dig in that closet to find them!), they could add them up and compare the sums. Students could also lay the rods end to end and see which side had the longer total length. These are all useful mathematical strategies, and we hope some of them emerge in your classroom.

But there is another avenue for compare the values (or lengths) on the two sides that leverages what is known as relational reasoning. We’ve written about relational reasoning before because it is such a powerful and efficient way of thinking. When using relational reasoning, students don’t need to ask themselves, What is the total on each side? Instead they look at the relationship between the component parts to see what is equal and what is not. In this image, students using relational reasoning might note that both the left and right sides have one purple rod, one yellow, rod, one dark green rod, and one light green rod. These are equal and do not change the relationship between the two sides. The difference between the two sides is that the left has a black rod and the right has a second dark green rod. Because the black rod is longer than the dark green rod, the value of the left side is greater. See how clever that is?

To help your students develop relational reasoning, ask the question, Which is more? with Cuisenaire rods or any of our other materials.

And we invite you to follow us on Twitter! Tweet us the fascinating ideas you students have about our activities or how you’re trying these activities in your space. We can’t wait to hear from you!

To multiplicity, cheers!

Jen Munson and the multiplicity lab group